软考高项-系统分析师--计算机组成结构(5. 校验码)
2024-03-29 10:01AM
校验码
码距:就单个编码A: 00而言,其码距为1,因为其只需要改变一位就变成另一个编码。在两个编码中,从A码到B吗转换所需要改变的位数称为码距,如A: 00要转换为B: 11,码距为2。一般来说,码距越大,越利于纠错和检错。
1. 奇偶校验码
奇偶校验码:在编码中增加1位校验位来使编码中的1个位数为奇数(奇校验)或者偶数(偶校验),从而使码距变为2。例如:
奇校验:编码中,含有奇数个1,发送给接收方,接收方收到后,会计算收到的编码有多少个1,如果是奇数个1,则无误,是偶数个,则有误。
偶校验同理,知识编码中有偶数个1,由上述,奇偶校验只能检1位错,并且无法纠错。
eg:校验码为:101110,我想要转换为奇校验
1)需要先查看101110里面有几个1,可以发现有4个1,4是偶数,要把偶数变为奇数。
2)所以再加一,为101110,1
如何想要把101110转换为偶校验,该如何修改?
1)需要先查看101110里面有几个1,可以发现有4个1,4是偶数,就不需要再加一了
2)所以再加0,为101110,0
2. CRC 循环冗余校验码
CRC只能检错,不能纠错。使用CRC编码,需要先约定一个生成多项是G(x)。生成多项式的最高位和最低位必须是1。假设原始信息有m位,则对应多项式M(x)。生成校验码思想就是在原始信息位后追加若干校验位,使得追加的信息能被G(x)整除。接收方接收到带校验位的信息,然后用G(x)整除。余数为0,则没有错误;反之则发生错误。
例:假设原始信息串为10110,CRC的生成多项式为G(x)=x^4+x+1,求CRC校验码。
1)在原始信息位后面添加0,假设生成多项式的阶为r,则在原始信息位后添加r个0,本题中,G(x)阶为4,则在原始信息位后面添0,假设生成多项式的阶为r,则在原始信息位后添加r个0,本题中,G(x)阶为4,则在原始信息串后加4个0,得到的新串为101100000,作为被除数。
2)由多项式得到除数,多项中x的幂指数存在的位置1,不存在的位置0。本题中,X的幂指数为0,1,4的变量都存在,而幂指数为2,3的不存在,因此得到串10011。(幂指数0存在,因为G(x)中有x^0(常数项1);幂指数1存在,因为G(x)中有x^1;幂指数3不存在,因为G(x)中没有x^3;幂指数4存在,因为G(x)中有x^4。)
3)生成CRC校验码,将前两步得出的被除数和除数进行模2除法运算(即不进位也不错位的除法运算)。模2运算就是“异或,就是同0非1”
同0非1:参与运算的两个数都是0的话,或者是相同的数,得出来的结果就是0,如果参与运算的两个数一个1,一个0,或者是不同的数,那么得出来的结果就是1。
除法过程如下图所示:
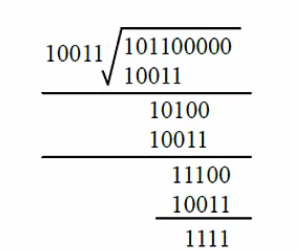
得到余数1111。
注意:余数不足r,则余数左边用若干个0补齐。如求得余数为11,r=4,则补两个0得到0011。
模2运算不进位也不借位,直接解,直接减,位数一致就可以算了
计算CRC步骤:
1.不需要管商,只要两个位数一样,就可以进行除法运算
2.模2运算,不进位,也不借位,直接减就可以了
不过:余数是有要求的,余位数一定是r位数,就是前面多项式的最高位数,多项式前面我们是4阶,它一定是4位数,不能是5位,也不能是3位
4)生成最终发送信息串,将余数添加到原始信息后。上例中,原始信息为10110,添加余数1111后,结果为101101111(前面四位是原始信息位,后面四位是校验位)。发送方将此数据发送给接收方。
5)接受方进行校验。接受方的CRC校验过程与生成过程类似,接受方接收了带校验位的帧后,用多项式G(x)来除。余数为0,则表示信息无错;否则要求发送方进行重传。
注意:收发信息双方需要使用相同的生成多项式。

3. 海明校验码
海明码:本质也是利用奇偶性来检错和纠错的检验方法,构成方法是在数据位之间的确定位置上插入k个校验位,通过扩大码距实现检错和纠错。
设数据位是n位,校验位是k位,则n和k必修满足一下关系:2^k-1>=n+k。
eg:求信息1011的海明码
3.1 校验位的位数和具体的数据位的位数之间的关系
所有位都编号,从最低位编号,从1开始递增,校验位处于2的n(n=0 1 2……)次方中,即处于第1,2,4,8,16,32,……位上,(注意这里是从1开始的,而不2)其余位才能填充真正的数据位,若信息数据位1011,则可知,第1,2,4位为校验位,第3,5,6,7位为数据位,用来从低位开始存放1011,得出信息位和校验位分布如下:
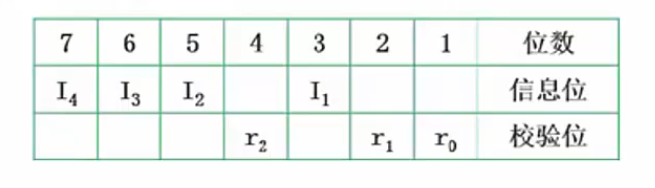
实际考试时可以依据公式 n+k<=2^k-1快速得出答案(n是已知的数据位个数,k是未知的校验位个数,依次取k=1代入计算,得出满足上式的最小的k的值)。
3.2 计算校验码
将所有信息位的编号都拆分成二进制表示,如下图所示:
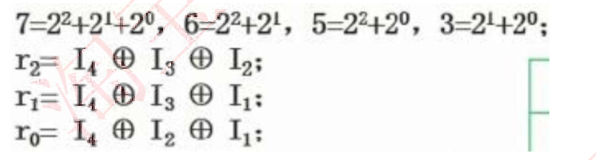
上图中,7=4+2+1,表示7由第4位校验位(r2)和第2校验位(r1)和第1校验位(r0)共同校验,同理,第6位数据位6=4+2,第5位数据位5=4+1,第3位数据位3=2+1,前面知道,这些2的n次方都是校验位,可知,第4位校验位的第7,6,5三位数据位,因此,第4位校验位r2等于这三位数据位的值异或,第2位和第1位校验位计算原理同上,最终得到如下:
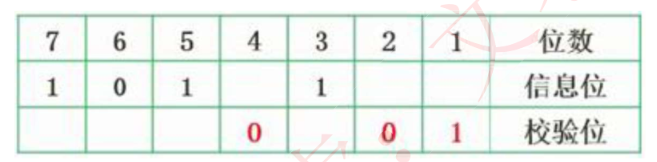
计算出3个校验位后,可知最终要发送的海明码校验为1010101。
3.3 检错和纠错原理
接收放收到海明码之后,会将每一位校验位与其他校验的位数分别异或,即做如下三组运算:

如果是偶校验,那么运算得到的结果应该全为0,如果是奇校验,应该全为1,才是正确(若采用奇校验,则前面计算校验码时需要将各校验位的偶校验值取反),假设是偶校验,且收到的数据位101110(第四位出错),此时,运算的结果为:

这里不全为0,表明传输过程有误,并且按照r2 r1 r0排列为二进制100,这里指出的就是错误位数,表示100,即第4位出错,找到了出错位,纠错方法就是将该位逆转。

校验码的考点:
1. 位数
2. 校验(考的很少,但是会有原理)
注意:以上内容都是参考文老师软考教育,我写在博客只是方便自己查看,记忆;如果想要看更完整内容,请去看文老师软考教育。
登录
请登录后再发表评论。
评论列表:
目前还没有人发表评论